I. Colinéarité
Dans un repère ![]() de l’espace, un vecteur
de l’espace, un vecteur ![]() est défini par ses trois coordonnées
est défini par ses trois coordonnées ![]() ,
, ![]() et
et ![]() (abscisse, ordonnée et cote). On utilise souvent la notation en colonne pour simplifier les calculs de proportionnalité :
(abscisse, ordonnée et cote). On utilise souvent la notation en colonne pour simplifier les calculs de proportionnalité :
![Rendered by QuickLaTeX.com \[\overrightarrow{u}\begin{pmatrix}x\\y\\z\end{pmatrix}\]](https://coetlogon.fr/wp-content/ql-cache/quicklatex.com-3f565f07aa45d0a2808f7420868f0bc1_l3.png)
De même que par deux points distincts ![]() et
et ![]() passe une unique droite, par trois points non alignés
passe une unique droite, par trois points non alignés ![]() ,
, ![]() ,
, ![]() passe un unique plan, que l’on peut noter
passe un unique plan, que l’on peut noter ![]() .
.
Colinéarité
Deux vecteurs
et
(avec
) sont dits colinéaires s’il existe un réel
tel que
.
Si deux vecteurs
et
sont non nuls et non colinéaires, on dit qu’ils forment une famille libre , notée
.
Deux vecteurs
et
ne formant pas une famille libre forment une famille liée
.
Remarques :
Dans ce qui suit, ![]() et
et ![]() sont deux vecteurs et
sont deux vecteurs et ![]() ,
, ![]() ,
, ![]() ,
, ![]() , quatre points.
, quatre points.
- Le vecteur nul
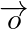 est colinéaire à tout autre vecteur.
est colinéaire à tout autre vecteur. - Lorsque
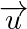 et
et 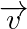 sont deux vecteurs non nuls, la colinéarité de
sont deux vecteurs non nuls, la colinéarité de 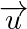 et
et 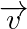 équivaut à la proportionnalité de leurs coordonnées.
équivaut à la proportionnalité de leurs coordonnées. - Pour démontrer que deux vecteurs non nuls
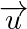 et
et 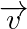 sont colinéaires, il suffit d’identifier le réel
sont colinéaires, il suffit d’identifier le réel 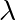 tel que de
tel que de 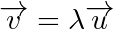 . Établir que deux vecteurs ne sont pas colinéaires est un peu plus délicat : pour justifier qu’il n’existe pas de tel réel
. Établir que deux vecteurs ne sont pas colinéaires est un peu plus délicat : pour justifier qu’il n’existe pas de tel réel 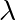 , on peut utiliser des déterminants.
, on peut utiliser des déterminants. 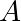 ,
, 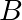 ,
,  sont alignés si et seulement si les vecteurs
sont alignés si et seulement si les vecteurs 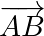 et
et 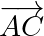 sont colinéaires.
sont colinéaires.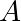 ,
, 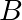 ,
,  sont alignés si et seulement si la famille
sont alignés si et seulement si la famille 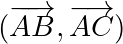 est liée.
est liée.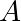 ,
, 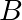 ,
,  forment un plan si et seulement si la famille
forment un plan si et seulement si la famille 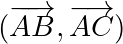 est libre.
est libre.- Deux droites
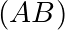 et
et 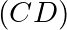 sont parallèles si et seulement si les vecteurs
sont parallèles si et seulement si les vecteurs 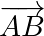 et
et 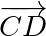 sont colinéaires.
sont colinéaires. - Un quadrilatère
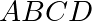 est un parallélogramme si et seulement si
est un parallélogramme si et seulement si 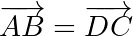 .
.
Question
Que dire d’un quadrilatère ![]() tel que
tel que ![]() et
et ![]() soient colinéaires ?
soient colinéaires ?
Représentation paramétrique d’une droite
Vecteur directeur d’une droite
Un vecteur non nul
dirige une droite
lorsqu’il existe deux points
et
de
tels que
.
On dit alors queest un vecteur directeur de
.
Remarques
- Si
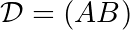 , alors
, alors 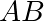 est un vecteur directeur de
est un vecteur directeur de 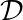 .
. - Si
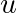 est un vecteur directeur de
est un vecteur directeur de 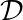 , alors tout vecteur
, alors tout vecteur 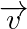 non nul et colinéaire à
non nul et colinéaire à  est également un vecteur directeur de
est également un vecteur directeur de 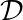 .
. - Réciproquement, deux vecteurs directeurs d’une même droite sont toujours colinéaires.
Repère d’une droite
Soit
une droite. Lorsque
est un point de
et
en est un vecteur directeur, on dit que le couple
est un repère de la droite
.
est alors l’origine de ce repère.
Représentation paramétrique d’une droite
La droite ![]() passant par
passant par ![]() et dirigée par
et dirigée par ![]() est l’ensemble des points
est l’ensemble des points ![]() tels que
tels que ![]() soit colinéaire à
soit colinéaire à ![]() .
.
En géométrie repérée, c’est-à-dire avec des coordonnées, la droite ![]() passant par
passant par ![]() et dirigée par
et dirigée par 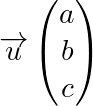 est l’ensemble des points
est l’ensemble des points ![]() de l’espace pour lesquels il existe un réel
de l’espace pour lesquels il existe un réel ![]() tel que
tel que
![Rendered by QuickLaTeX.com \[\begin{cases} x = x_A + \lambda a \\ y = y_A + \lambda b \\ z = z_A + \lambda c \end{cases}.\]](https://coetlogon.fr/wp-content/ql-cache/quicklatex.com-d4d571ad7b557475a50fbef566c7558c_l3.png)
On parle d’une représentation paramétrique de ![]() ; c’est la représentation paramétrique de
; c’est la représentation paramétrique de ![]() associée au repère
associée au repère ![]() .
.
On note
![Rendered by QuickLaTeX.com \[\mathcal{D}:\begin{cases} x = x_A + \lambda a \\ y = y_A + \lambda b \\ z = z_A + \lambda c \end{cases} (\lambda\in\mathbb{R})\]](https://coetlogon.fr/wp-content/ql-cache/quicklatex.com-c06f9c84fe3d77329b82d0001344f575_l3.png)
Coplanarité
Quatre points
,
,
,
sont dits coplanaires s’il existe un plan contenant ces quatre points.
Remarque
Lorsque ![]() ,
, ![]() ,
, ![]() ne sont pas alignés, ceci équivaut à dire que
ne sont pas alignés, ceci équivaut à dire que ![]() .
.
Lorsque trois points
,
,
ne sont pas alignés, on dit que la famille libre
est une base du plan
et que le triplet
en est un repère.
On dit aussi, enfin, que les vecteurset
dirigent le plan.
Remarque
Autrement dit, un point ![]() et deux vecteurs
et deux vecteurs ![]() et
et ![]() non colinéaires étant donnés, on peut parler du plan passant par
non colinéaires étant donnés, on peut parler du plan passant par ![]() et dirigé par
et dirigé par ![]() et
et ![]() .
.
Théorème
Soient
,
,
trois points non alignés. Pour tout point
du plan
, il existe un unique couple
de réels tel que
.
Remarque
Les réels ![]() et
et ![]() s’interprètent comme les coordonnées du point
s’interprètent comme les coordonnées du point ![]() dans le repère
dans le repère ![]() du plan
du plan ![]() .
.
Preuve du théorème
Existence
Soit ![]() un point du plan
un point du plan ![]() et soit
et soit ![]() la droite parallèle à
la droite parallèle à ![]() passant par
passant par ![]() . Par hypothèse, les vecteurs
. Par hypothèse, les vecteurs ![]() et
et ![]() ne sont pas colinéaires, donc les droites
ne sont pas colinéaires, donc les droites ![]() et
et ![]() sont sécantes, donc les droites
sont sécantes, donc les droites ![]() et
et ![]() sont également sécantes.
sont également sécantes.
Notons ![]() le point d’intersection de
le point d’intersection de ![]() et
et ![]() .
.
La relation de Chasles donne ![]() .
.
Or, puisque ![]() ,
, ![]() est colinéaire à
est colinéaire à ![]() : il existe un réel
: il existe un réel ![]() tel que
tel que ![]() .
.
De même, puisque ![]() et
et ![]() sont deux point d’une parallèle à
sont deux point d’une parallèle à ![]() ,
, ![]() est colinéaire à
est colinéaire à ![]() et donc il existe un réel
et donc il existe un réel ![]() tel que
tel que ![]() .
.
On obtient bien :
![]()
Unicité
Supposons disposer de deux décompositions de ![]() comme combinaison linéaire de
comme combinaison linéaire de ![]() et
et ![]() , disons
, disons ![]() et
et ![]() , où
, où ![]() ,
, ![]() ,
, ![]() , \mu’
, \mu’![]() \lambda\overrightarrow{AB}+\mu\overrightarrow{AC}=\lambda’\overrightarrow{AB}+\mu’\overrightarrow{AC}
\lambda\overrightarrow{AB}+\mu\overrightarrow{AC}=\lambda’\overrightarrow{AB}+\mu’\overrightarrow{AC}![]() \lambda\overrightarrow{AB}-\lambda’\overrightarrow{AB}=\mu’\overrightarrow{AC}-\mu\overrightarrow{AC}
\lambda\overrightarrow{AB}-\lambda’\overrightarrow{AB}=\mu’\overrightarrow{AC}-\mu\overrightarrow{AC}![]() (\lambda-\lambda’)\overrightarrow{AB}=(\mu’-\mu)\overrightarrow{AC}
(\lambda-\lambda’)\overrightarrow{AB}=(\mu’-\mu)\overrightarrow{AC}![]() \overrightarrow{AB}
\overrightarrow{AB}![]() \overrightarrow{AC}
\overrightarrow{AC}![]() \lambda-\lambda’=0
\lambda-\lambda’=0![]() \mu’-\mu=0
\mu’-\mu=0![]() \lambda=\lambda’
\lambda=\lambda’![]() \mu=\mu’$.
\mu=\mu’$.
Ceci démontre l’unicité.